测试
1.1 位置和姿态¶
在机器人学中,描述一个空间物体需要明确其 位置(position) 和 姿态(Posture) ,二者共同定义了物体在三维空间中的完整状态。
描述物体在空间中的位置和姿态需要建立一个参考坐标系,一般称为 世界坐标系 。基于这个世界坐标系:
- 描述物体在空间的 坐标点 ,即位置。
- 描述物体在空间的 朝向或旋转状态 ,即姿态。
1.2 正逆运动学¶
1.2.1 正运动学¶
正运动学 是基于一组关节角计算出 末端执行器相对于机械臂基坐标的位置和姿态 。
1.2.2 逆运动学¶
逆运动学 是基于末端执行器的位置和姿态计算出 所有可达给定位置和姿态的关节角 。
1.3 奇异点¶
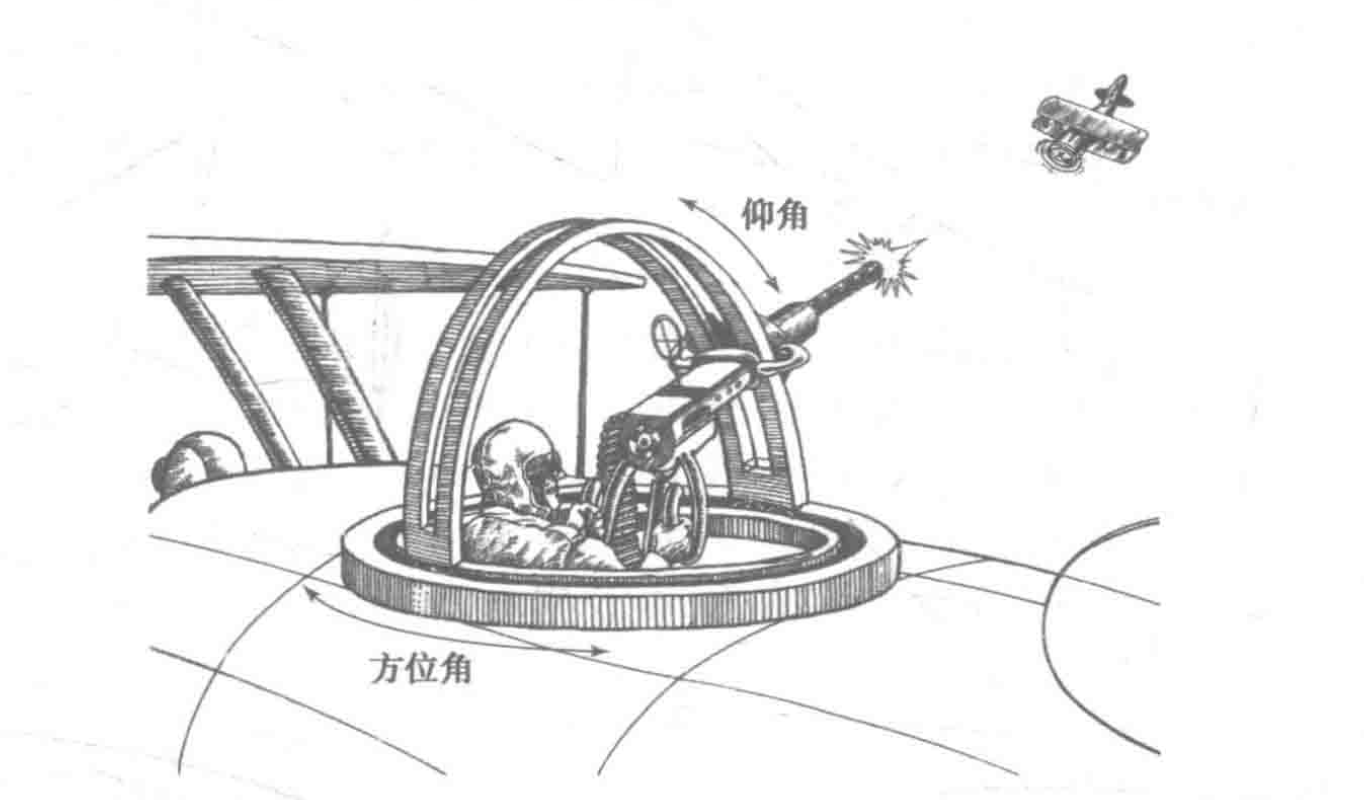
奇异点 是指机器人运动到特定空间位置和姿态下,会导致机器人失去一个或多个自由度。
如下图所示是一个飞机上的机枪机构,有方位角和仰角两个自由度,几乎可以射击整个上半球的任意目标。但是,当敌机水平从机构头顶飞过时,机枪的仰角慢慢接近 90°,短时间内机构缺失一个自由度,无论怎么切换方位角,此时射击范围都难以改变。
1.4 动力学¶
1.5 轨迹规划¶
平稳控制机械臂从起点运动至终点,并非简单指定终点坐标即可实现,而是需要为每个关节规划特定的时间连续函数。通常,机械臂所有关节需满足同步启停要求。 轨迹规划 的核心任务,正是求解这些满足运动约束的时间连续函数。
1.6 符号表示¶
- 一般大写字母的变量表示矢量或矩阵小写字母的变量表示标量。
- 左下标和左上标表示变量所在的坐标系。
- 右上标用来表示矩阵的逆或转置。
需要注意:
- $ ^{A}{P} $表示坐标系 A 下的位置矢量。
- $ _{B}^{A}R $表示坐标系 B 相对于坐标系 A 的*姿态的旋转矩阵*。
:::danger 危险
:::